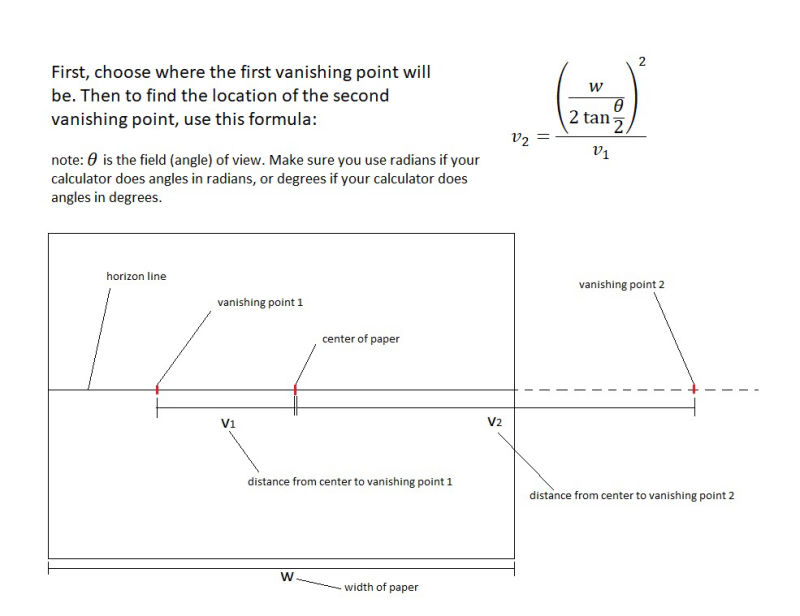
Formula for the location of vanishing points
-
I don't know if anyone will actually use this, but I worked out a formula for where to put vanishing points in 2-point perspective. I watched several of the SVS courses that teach perspective and noticed that there were several questions about how you know exactly where the vanishing points are supposed to go. The general answer seemed to be to start drawing the cube, or building, or whatever it is that you are drawing and when it looks "right" you can figure out where the vanishing points are based on what you have already drawn. I totally agree with the instructors that the best and most efficient way to do this is to get a feel for it and to be able to draw with perspective that looks "close enough" so that it looks good. But the question stilled nagged at me and I thought that there must be some way to figure out the exact, correct place to put vanishing points.
I did some googling and found a cool tutorial about 2-point perspective at http://guidetodrawing.com/linear-perspective/two-point-perspective/ . This shows how to start with a top down view of a building and then draw it in perspective, and it explains how to find the vanishing points based on the top down view. But I wanted to a way to figure out the location of the vanishing without going through the whole top down view process. So I did some math and worked out the formula in the image below.
In this formula, w is the width of your paper, theta is your field of view, and v1 is the distance from the center of your horizon line to your first vanishing point. Yes, you have to choose what field of view you want and where one of the vanishing points is. But the formula should always spit out the distance from the center of the horizon line to the second vanishing point to give you totally accurate perspective. The formula should work when both vanishing points are on the paper, when one is on the paper and one is off, and when both vanishing points are off the paper. According to the wikipedia article about field of view, 84-114 degrees is "ultra wide angle," 64-84 degrees is "wide angle" and "normal" is 40-62 degrees. So your drawing will look most natural if your field of view is 40 to 62 degrees.
-
@dlarmantrout Brilliant!! Here is an ex-scientist who loves perspective and I’m definitely going to try this out.
So far I´ve gone the super lazy way: find a photo that has the perspective you want and take the vanishing point position from it.
There is one baffling element missing if you want to set up a perfect grid from scratch: the depth of the perfect square. That goes in line with the field of view and there are ways to determine it geometrically but they are complex. Can you put your mind to sorting that out? :-)) -
My heart is willing but my mind is getting in the way
 . I got A’s in art and C’s in math.
. I got A’s in art and C’s in math.
Please explain what “tan” is?
Once that is out of the way I will probably have more questions .
. -
@burvantill tan is short for "tangent," which is a trigonometric function. It has a different meaning in this context than in the context of composition, where tangent means things that are touching on the edge. Scientific calculators should have a "tan" button and you can even find a tangent right in the Google search bar. Try typing "tan(45)" into Google and it will bring up a little calculator that tells you the answer. The number you put in the tan() parentheses is an angle. In the vanishing point formula, the angle you use is half of the field of view. You have to make sure the calculator is set to degrees if you are entering the angle in degrees. In the Google calculator there is a slider that lets you switch from radians to degrees.
I know using the formula is complicated : ) That's why everyone just eyeballs it. This is more than you need to know, but the tangent of an angle is equal to, when the angle is one of the angles in a right triangle, the length of the side of the triangle opposite from the angle divided by the length of the side of the triangle adjacent to the angle.
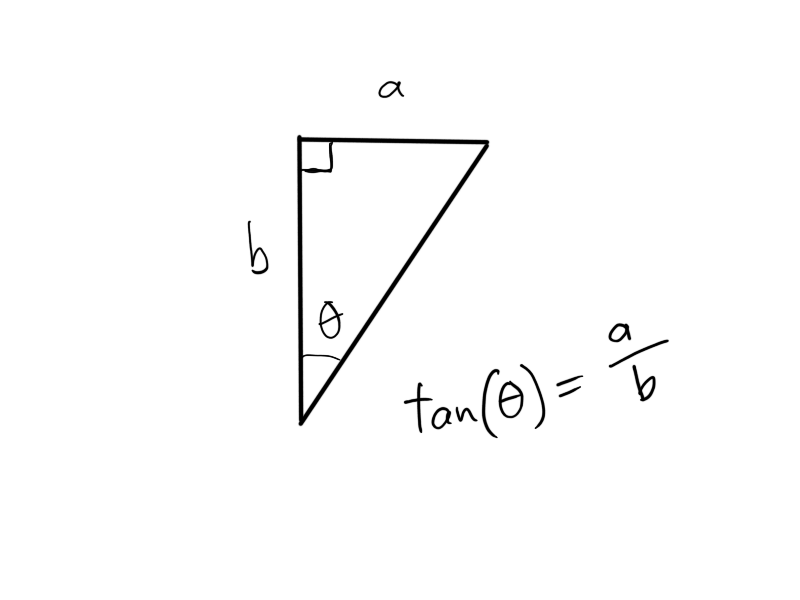
-
@smceccarelli Good idea! Having an accurate grid would make it easy to place things where you want in the picture. I think what you're asking is if you want to draw a perfect square in perspective, and you draw one side of the square (you can arbitrarily decide how long to make the first side since you are choosing the size of the square), then how do you know how long to make the next side of the square so that it actually is a square and not a rectangle? That is a good question and I'm sure there is a way to figure that out. I'll think about it. Once you have one perfect square drawn you should be able to expand it to a grid of any size you want by drawing lines through the midpoint of the sides like Jake does with telephone poles or fence posts in the perspective course.
-
@dlarmantrout Exactly! The perfect square is the key to correct perspective in line with the chosen field of view and normally I wing it. The key is the position of the diagonal vanishing point (DVP), the vanishing point of the diagonal of the square (or the 45° lines).
Here is a scan from "Vanishing Point" - an excellent book on perspective by Jason Cheeseman-Meyer, that talks about the relation between field-of-view and DVP. It's quite obvious with one-point perspective, but not so trivial with 2-point perspective (I'm not sure I ever learnt how to do it, and if I did I forgot...)
Given that you have a formula for the second vanishing point (i.e. the 90° line to the first), it should be relatively easy to work out a formula for the vanishing point of the 45° line)...
-
@burvantill I'd be lucky to get C's in math! In my world, that actually qualifies you as a Math Whiz.

-
My head just exploded.


Thank you for answering my question. I'm going to have to reread this many times, but I like learning new things so I'm going to try it out. I'll need to get one of those doohickies, a protractor?? -
@eli LOL! Thanx! My son would disagree with you. He hates it when I help him with his math homework, because he always seems to know more and ends up teaching me. Lol! If I master this technique it will impress the hell out of him.

-
@burvantill Don´t worry - this is a disease, not an asset. It´s called “incurable nerdyness”. It keeps your mind from just relaxing and doing great art, is a big enemy of instinct and innate skills (which it fundamentally mistrusts) and I’m pretty sure it´s responsible for the fact that I have such a hard time writing fiction...
Believe me, you don’t need maths to do great perspective drawings! It´s just the peculiar way people who have this disease go about things... -
Thank you
-
I'm also one of those "not so great at math but still nerdy enough to want to try this" so my question is: in your formula where w = width of paper, and the v's are the vanishing points, what is your measurement unit (metric?) or can you use any unit as long as you are consistent? Or have I so completely misunderstood the formula that my question doesn't even make sense?

-
@smceccarelli Yep, this was all due to my incurable nerdyness making me want to find the exact right answer. If I were teaching a class on drawing in perspective and someone asked how do know where to put the vanishing points, I would probably say... "There is a way to figure out the exact spot, but TRUST ME, you would rather just do it by feel." With that said, I am trying to a work out a formula for the diagonal vanishing point. And then maybe the 3rd vanishing point for 3-point perspective.
-
@demotlj You can use any units as long as you are consistent. The w is the width of the paper and v1 and v2 are the distance from the center point of the horizon line to each vanishing point (v1 on the left and v2 on the right)
-
@smceccarelli Apologies for necroing this thread - but this phrasing cracked me up so hard!
 I'm doing the basic perspective course but my (ex)physicist brain wasn't satisfied until I figured out exactly how to draw a room if I'm standing at a specific point inside it and as a result I've spent (way waaay) too much time drawing triangles.
I'm doing the basic perspective course but my (ex)physicist brain wasn't satisfied until I figured out exactly how to draw a room if I'm standing at a specific point inside it and as a result I've spent (way waaay) too much time drawing triangles.  And then this came up as I was googling, as an, ahem, gentle reminder to stop obsessing and start, you know, drawing.
And then this came up as I was googling, as an, ahem, gentle reminder to stop obsessing and start, you know, drawing. 
-
Whoa this is brilliant! I was just thinking this the other day. I’ll read shortly (count me in as not so great at math).
-
@danielerossi As much as it pains my nerd heart to admit it, I don't think it's worth going through the maths. Unless you want to do highly technical illustrations.
-
@ina No worries. It was a fun read but in the end, I agree, best to eyeball it

-
@ina @danielerossi This is hilarious! Reminds me of a beginner animation class I had, first day our teacher (a hippie type) said when animating a bouncing ball (literally first exercise ever) each rebound would be about half the height of the previous rebound. A student raised his hand and started explaining the actual physics behind this and the exact formula to calculate the real height the ball would be after each rebound. You should have seen the teacher's eyes glaze over! Everyone in the class was frowning and giving each other side eye like "this is going to be a long semester". When the student was done, the teacher just said "Huuuhh, yeah.. I guess.." and resumed his lesson

-